elipse

La elipse posee un «eje mayor», trazo AB (que equivale a ), y un «eje menor», trazo CD (que equivale a 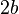); la mitad de cada uno de esos ejes recibe el nombre de «semieje», de tal manera que se los denomina «semieje mayor» y «semieje menor», respectivamente.
Sobre el «eje mayor» existen dos puntos y que se llaman «focos».
El punto es uno que pertenezca a la «elipse».

[editar] Puntos de una elipse

Si F₁ y F₂ son dos puntos del plano y d es una constante mayor que la distancia F₁ F₂, un punto Q pertenecerá a la elipse, si: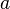

donde es el semieje mayor de la elipse.

[editar] Ejes de una elipse

Eje mayor (2 a) es la distancia mayor entre dos puntos adversos. En la figura, longitud del segmento AB.
La medida a es la mitad del eje mayor, o sea es el semieje mayor. La distancia del centro de la elipse al punto A o al punto B.
El resultado constante de la suma de las distancias de cualquier punto a los focos equivale al eje mayor.
Obsérvese que d(AF₂) + d (AF₁) = d(AF₂) + d (BF₂)= AB
La medida b es la mitad del eje menor, o sea es el semieje menor, la distancia del centro al punto C o al punto D.

[editar] Excentricidad de una elipse

La excentricidad de una elipse es la razón entre su semidistancia focal (segmento que va del centro de la elipse a uno de sus focos), denominada por la letra 'c', y su semieje mayor. Su valor se encuentra entre cero y uno.